# <img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/matrex_logo_dark_rounded.png" width="50px" /> Matrex
[](https://travis-ci.org/versilov/matrex)
[](https://coveralls.io/github/versilov/matrex?branch=master)
[](http://inch-ci.org/github/versilov/matrex)
[](https://hex.pm/packages/matrex)
Fast matrix manipulation library for Elixir implemented in C native code with highly optimized CBLAS sgemm() used for matrix multiplication.
For example, vectorized linear regression is about 13 times faster, than Octave single threaded implementation.
It's also memory efficient, so you can work with large matrices,
about billion of elements in size.
Based on matrix code from https://github.com/sdwolfz/exlearn
## Benchmark
#### Comparison with pure Elixir libraries
Slaughter of the innocents, actually.
2015 MacBook Pro, 2.2 GHz Core i7, 16 GB RAM
Dot product of 500x500 matrices
| Library | Ops/sec | Compared to Matrex |
| ------------ | -------- | ------------------- |
| Matrex | 674.70 | |
| Matrix | 0.0923 | 7 312.62× slower |
| Numexy | 0.0173 | 38 906.14× slower |
| ExMatrix | 0.0129 | 52 327.40× slower |
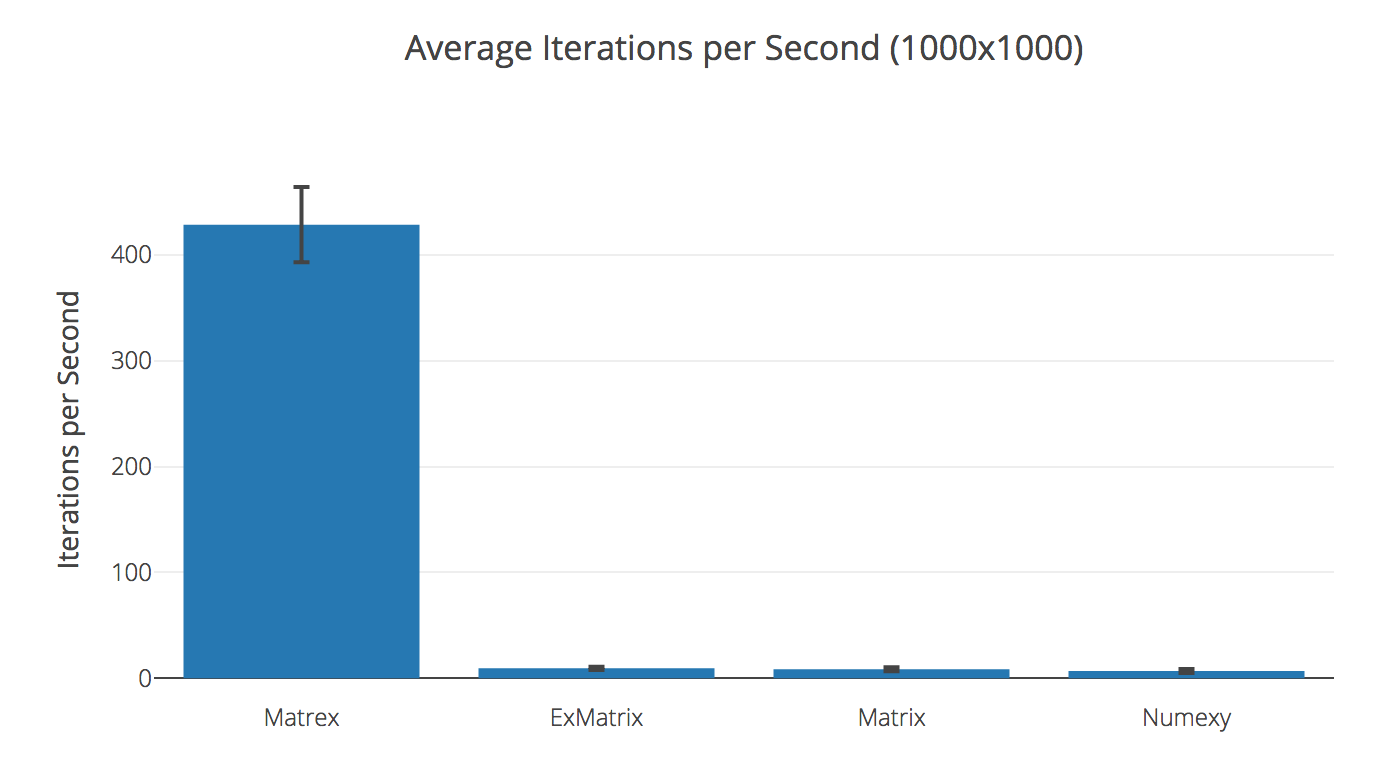
Transposing 1000x1000 matrix
| Library | Ops/sec | Compared to Matrex |
| ------------ | -------- | ------------------- |
| Matrex | 428.69 | |
| ExMatrix | 9.39 | 45.64× slower |
| Matrix | 8.54 | 50.17× slower |
| Numexy | 6.83 | 62.80× slower |
## Example
Complete example of Matrex library at work:
[Linear regression on MNIST digits (Jupyter notebook)](https://github.com/versilov/matrex/blob/master/Matrex.ipynb)
## Visualization
Matrex implements `Inspect` protocol and looks nice in your console:
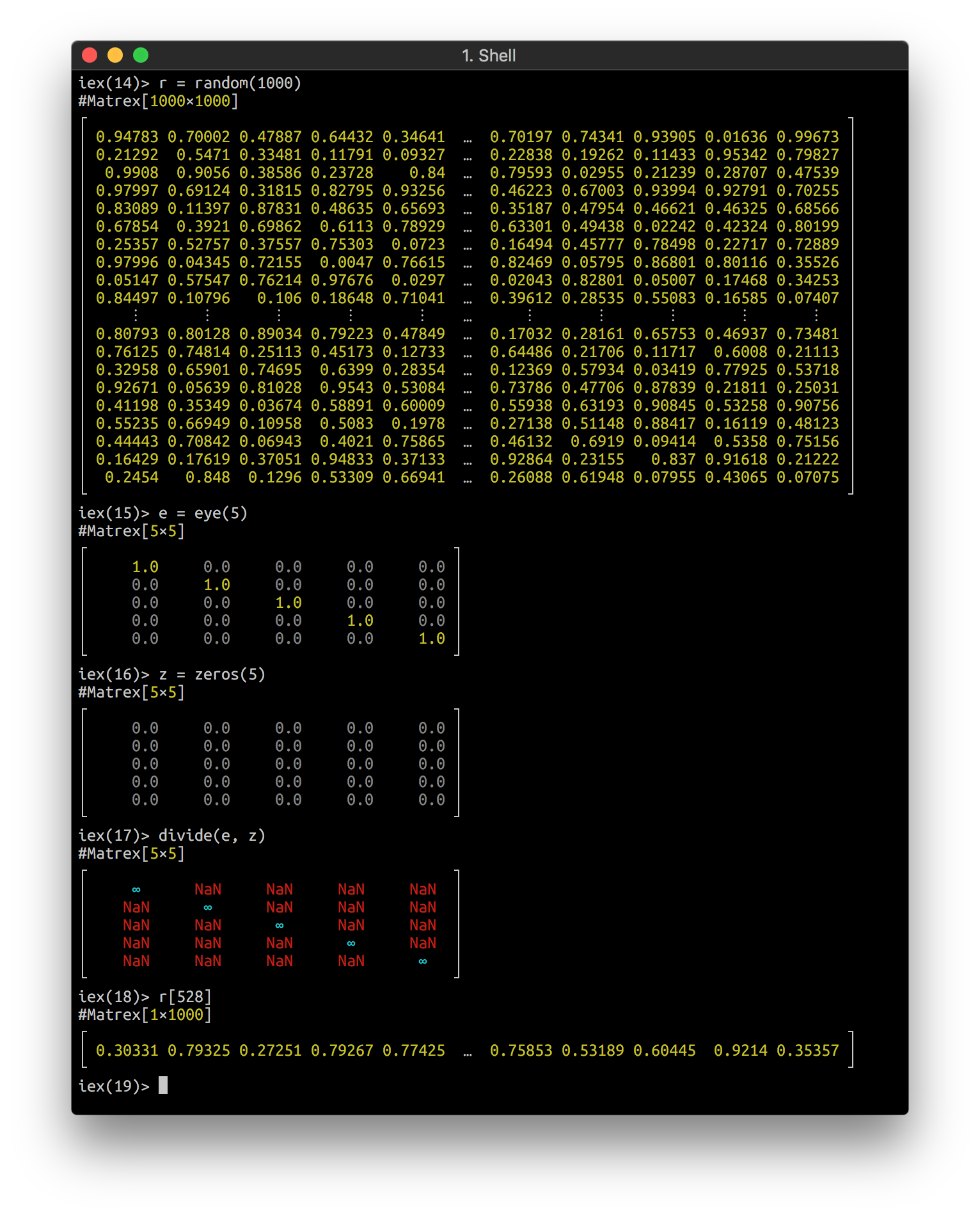
It can even draw a heatmap of your matrix in console! Here is an animation of logistic regression training with Matrex library and some matrix heatmaps:
<img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/mnist8.png" width="200px" />
<img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/mnist_sum.png" width="200px" />
<img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/magic_square.png" width="200px" />
<img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/hot_boobs.png" width="220px" />
<img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/neurons_mono.png" width="233px" />
<img src="https://raw.githubusercontent.com/versilov/matrex/master/docs/logistic_regression.gif" width="180px" />
## Installation
The package can be installed
by adding `matrex` to your list of dependencies in `mix.exs`:
```elixir
def deps do
[
{:matrex, "~> 0.6"}
]
end
```
### MacOS
Everything works out of the box, thanks to Accelerate framework.
### Ubuntu
You need to install scientific libraries for this package to compile:
```bash
> sudo apt-get install build-essential erlang-dev libatlas-base-dev
```
### Windows
It will definitely work on Windows, but we need a makefile
and installation instruction. Please, contribute.
## Access behaviour
Access behaviour is partly implemented for Matrex, so you can do:
```elixir
iex> m = Matrex.magic(3)
#Matrex[3×3]
┌ ┐
│ 8.0 1.0 6.0 │
│ 3.0 5.0 7.0 │
│ 4.0 9.0 2.0 │
└ ┘
iex> m[2][3]
7.0
```
Or even:
```elixir
iex> m[1..2]
#Matrex[2×3]
┌ ┐
│ 8.0 1.0 6.0 │
│ 3.0 5.0 7.0 │
└ ┘
```
There are also several shortcuts for getting dimensions of matrix:
```elixir
iex> m[:rows]
3
iex> m[:size]
{3, 3}
```
calculating maximum value of the whole matrix:
```elixir
iex> m[:max]
9.0
```
or just one of it's rows:
```elixir
iex> m[2][:max]
7.0
```
calculating one-based index of the maximum element for the whole matrix:
```elixir
iex> m[:argmax]
8
```
and a row:
```elixir
iex> m[2][:argmax]
3
```
## Math operators overloading
`Matrex.Operators` module redefines `Kernel` math operators (+, -, *, / <|>) and
defines some convenience functions, so you can write calculations code in more natural way.
It should be used with great caution. We suggest using it only inside specific functions
and only for increased readability, because using `Matrex` module functions, especially
ones which do two or more operations at one call, are 2-3 times faster.
### Usage example
```elixir
def lr_cost_fun_ops(%Matrex{} = theta, { %Matrex{} = x, %Matrex{} = y, lambda } = _params)
when is_number(lambda) do
# Turn off original operators
import Kernel, except: [-: 1, +: 2, -: 2, *: 2, /: 2, <|>: 2]
import Matrex.Operators
import Matrex
m = y[:rows]
h = sigmoid(x * theta)
l = ones(size(theta)) |> set(1, 1, 0.0)
j = (-t(y) * log(h) - t(1 - y) * log(1 - h) + lambda / 2 * t(l) * pow2(theta)) / m
grad = (t(x) * (h - y) + (theta <|> l) * lambda) / m
{scalar(j), grad}
end
```
The same function, coded with module methods calls (2.5 times faster):
```elixir
def lr_cost_fun(%Matrex{} = theta, { %Matrex{} = x, %Matrex{} = y, lambda } = _params)
when is_number(lambda) do
m = y[:rows]
h = Matrex.dot_and_apply(x, theta, :sigmoid)
l = Matrex.ones(theta[:rows], theta[:cols]) |> Matrex.set(1, 1, 0)
regularization =
Matrex.dot_tn(l, Matrex.square(theta))
|> Matrex.scalar()
|> Kernel.*(lambda / (2 * m))
j =
y
|> Matrex.dot_tn(Matrex.apply(h, :log), -1)
|> Matrex.subtract(
Matrex.dot_tn(
Matrex.subtract(1, y),
Matrex.apply(Matrex.subtract(1, h), :log)
)
)
|> Matrex.scalar()
|> (fn
:nan -> :nan
x -> x / m + regularization
end).()
grad =
x
|> Matrex.dot_tn(Matrex.subtract(h, y))
|> Matrex.add(Matrex.multiply(theta, l), 1.0, lambda)
|> Matrex.divide(m)
{j, grad}
end
```
## Enumerable protocol
Matrex implements `Enumerable`, so, all kinds of `Enum` functions are applicable:
```elixir
iex> Enum.member?(m, 2.0)
true
iex> Enum.count(m)
9
iex> Enum.sum(m)
45
```
For functions, that exist both in `Enum` and in `Matrex` it's preferred to use Matrex
version, beacuse it's usually much, much faster. I.e., for 1 000 x 1 000 matrix `Matrex.sum/1`
and `Matrex.to_list/1` are 438 and 41 times faster, respectively, than their `Enum` counterparts.
## Saving and loading matrix
You can save/load matrix with native binary file format (extra fast)
and CSV (slow, especially on large matrices).
Matrex CSV format is compatible with GNU Octave CSV output,
so you can use it to exchange data between two systems.
### Example
```elixir
iex> Matrex.random(5) |> Matrex.save("rand.mtx")
:ok
iex> Matrex.load("rand.mtx")
#Matrex[5×5]
┌ ┐
│ 0.05624 0.78819 0.29995 0.25654 0.94082 │
│ 0.50225 0.22923 0.31941 0.3329 0.78058 │
│ 0.81769 0.66448 0.97414 0.08146 0.21654 │
│ 0.33411 0.59648 0.24786 0.27596 0.09082 │
│ 0.18673 0.18699 0.79753 0.08101 0.47516 │
└ ┘
iex> Matrex.magic(5) |> Matrex.divide(Matrex.eye(5)) |> Matrex.save("nan.csv")
:ok
iex> Matrex.load("nan.csv")
#Matrex[5×5]
┌ ┐
│ 16.0 ∞ ∞ ∞ ∞ │
│ ∞ 4.0 ∞ ∞ ∞ │
│ ∞ ∞ 12.0 ∞ ∞ │
│ ∞ ∞ ∞ 25.0 ∞ │
│ ∞ ∞ ∞ ∞ 8.0 │
└ ┘
```
## NaN and Infinity
Float special values, like `:nan` and `:inf` live well inside matrices,
can be loaded from and saved to files.
But when getting them into Elixir they are transferred to `:nan`,`:inf` and `:neg_inf` atoms,
because BEAM does not accept special values as valid floats.
```elixir
iex> m = Matrex.eye(3)
#Matrex[3×3]
┌ ┐
│ 1.0 0.0 0.0 │
│ 0.0 1.0 0.0 │
│ 0.0 0.0 1.0 │
└ ┘
iex> n = Matrex.divide(m, Matrex.zeros(3))
#Matrex[3×3]
┌ ┐
│ ∞ NaN NaN │
│ NaN ∞ NaN │
│ NaN NaN ∞ │
└ ┘
iex> n[1][1]
:inf
iex> n[1][2]
:nan
```
